Summer School Part 1 - Max Flow Min Cut Problem

KAIST opened a 5 day summer school from July 22nd to 25th with the topics of combinatorics and algorithms. I got to know about this through a friend, and once I heard about it, there was no way I wasn’t going. So I went, along with some of my friends, and it was a blast. I learnt so many new things with so much depth, from stuff I have heard of to things I have never known even existed. I also got to meet and talk with people who were experts on the field. Overall all the lectures were super fun and interesting, and once it was all over, all I wanted was for it to last a little longer.

Everyday there were two lectures from two professors, except on the first day where only one professor gave the lecture. Professor Chien-Chung Huang’s lecture was on combinatorial optimization, where he taught about flows and cuts, matching problems, matroids, and Gomory-Hu trees. Professor Sebastian Wiederrecht’s lecture was called From treewidth to grid minor theorem, where he taught about tree decompositions, tree width, grid minor theorem, and so on. At the end of each day, excluding the last day, we were handed out a few exercises to think and solve with in a group of at most six, and an hour where each group could share their solutions and thoughts.

Starting from this post, I plan on uploading a total of 9 posts(could be less, could be more) where I try to organize everything I have learnt, because I learnt a lot, and strongly felt the need to organize everything. Each post will contain the stuff taught from each lecture on each day by one of the professors. More specifically, I plan to organize everything like the following:

The max flow - min cut problem
Matching in bipartite graphs
Matching in general graphs
Matroids
The Gomory-Hu tree
Tree decomposition and treewidth
Computing tree decompositions of small width
The grid theorem
Exluding odd structures

The first 5 are from the lecture by Chien-Chung Huang, and the latter 4 are from the lecture by Sebastian Wiederrecht. This is kind of ambitious for me, but I think I can get it done. I also plan to explain the practice problems given, but there are problems that I wasn’t able to solve. Now without further ado, lets begin.

Introduction

This post will be looking at the max flow - min cut problem. We start by defining the problem, then looking at some theorems on solving the problem. We then look at an algorithm called the Preflow-Push Algorithm (also known as the Push-Relabel Algorithm) that solves the max flow problem, as well as prove why it works.

Problem Definition

We start by defining the max flow and min cut problems, starting with max flow.

Given a graph $G = (V,E)$ with directed edges and capacities $c : E \rightarrow \mathbb{R}_ {>0}$, and two terminal vertices $s, t \in V$, we say $f : E \rightarrow \mathbb{R}_{>0}$ is a flow if $f$ holds the following conditions.

$0 \leq f(e) \leq c(e) \quad ^\forall e \in E$
$\sum_{\delta^+(v)} f(e) = \sum_{\delta^-(v)} f(e) \quad ^\forall v \in V \ {s,t}$

Where $\delta^+(v)$ are the edges going out of $v$ and $\delta^-(v)$ are the edges going into $v$. We define the flow value of $f$ as the following.

\[\|f\| = \sum_{e \in \delta^+(s)} f(e) - \sum_{e \in \delta^-(s)} f(e)\]

Finally, the Max flow problem is the problem where we want to find a flow $f$ so that $|f|$ is maximized.

Lets now look at the min cut problem.

Again we have the same graph and capacities from the max flow problem. We call a set of vertices $C \subset V$, where $s \in C$ and $t \notin C$ a cut (more specifically a $s,t$ - cut). Here, we define the cut value of $C$ as the following.

\[\|C\| = \sum_{e \in \delta^+(c)} c(e)\]

This is the essentially the sum of edges removed in order to get rid of all paths from $s$ to $t$. Like the max flow problem, the min cut problem is the problem where we want to find a cut $C$ so that $|C|$ is minimized.

Here, we can make a proposition:

Proposition: Given any $X \subset V$, where $s \in X$ and $t \notin X$, then the flow value can be written as $|f| = \sum_{e \in \delta^+(X)} f(e) - \sum_{e \in \delta^-(X)} f(e)$

Proof: This is a simple double counting argument, since the our original definition of $|f|$ can be written as the following:

\[\|f\| = \sum_{v \in X} \left( \sum_{e \in \delta^+(v)} f(e) - \sum_{e \in \delta^-(v)} f(e) \right)\]

since the flow value is the amount of flow going out of $X$ minus the amount of flow coming into $X$. $\blacksquare$

Notice how the righthand side of the equation given in the proposition will always be less than cut value $|X|$, since the flow is less than the capacity, and we subtract some stuff. This observation can lead us to the following.

Corollary: Given any flow $f$ and cut $C$, $|f| \leq |C|$

This corollary gives us the weak duality of the max flow problem and the min cut problem. In fact, if you know about strong duality, the two values are the always the same.

The Residual Network

We are now going to create a new network based on the original graph called a residual network, which we will call the residual network.

Given a flow $f$, we will create a new graph $G(f) = (V,F)$ where $F$ is generated as follows. Given an edge $e = (u,v) \in E$,

Create an edge $(u,v) \in F$ if $c(e) - f(e) > 0$, with a weight of $u(e) = c(e) - f(e)$
Create an edge $(v,u) \in F$ if $f(e) > 0$, with a weight of $u(e) = f(e)$

Here, we call a path $P$ in $G(f)$ an augmenting path if $P$ is a path form $s$ to $t$ in $G(f)$. We can make a proposition using the augmenting path.

Proposition: If a flow $f$ is augmented along an augmenting path $P$ in $G(f)$ with the amount $\min{u(e)}$ the result is a new flow of value $\min{u(e)}$ extra

This should be pretty obvious, I think. Using the proposition above, we can construct an algorithm for finding the max flow, though it does look a bit naive.

Algorithm

Initialization: $f \equiv 0$
While $G(f)$ has an augmenting path $P$, augment $f$ along $P$

Now lets prove this algorithm works. To show that the resulting flow from the algorithm is maximum, we show that there exists a cut with the same cut value. Then, by the weak duality we proved earlier, we can know for a fact that the flow is maximum.

Theorem(Ford-Fulkerson, 1965): When the algorithm stops, $f$ is the max flow

Proof: Since the algorithm stops there is no more augmenting paths in $G(f)$. Let $X$ be the set of reachable vertices from $s$ in $G(f)$. Then, by our proposition from above, the following is true:

\[\|f\| = \sum_{e \in \delta^+(X)} f(e) - \sum_{e \in \delta^-(X)} f(e)\]

Since there is no augmenting path in $G(f)$, there should only be edges going from $V / X$ to $X$. In other words, for all edges $e \in G$ going from $X$ to $V / X$, $f(e) = c(e)$, and for all edges $e \in G$ going from $V/X$ to $X$, $f(e) = 0$. Therefore $\sum_{e \in \delta^-(X)} f(e) = 0$, and $|f| = \sum_{e \in \delta^+(X)} f(e) = \sum_{e \in \delta^+(X)} c(e) = |X|$. In other words, once the algorithm stops, there exists a cut with the same value as the flow, making the flow maximum. $\blacksquare$

How efficient is this algorithm? Not super good. Since there is no criteria on what augmenting path to choose, our algorithm might continuously choose a not-so-good augmenting path. The following image shows an example.

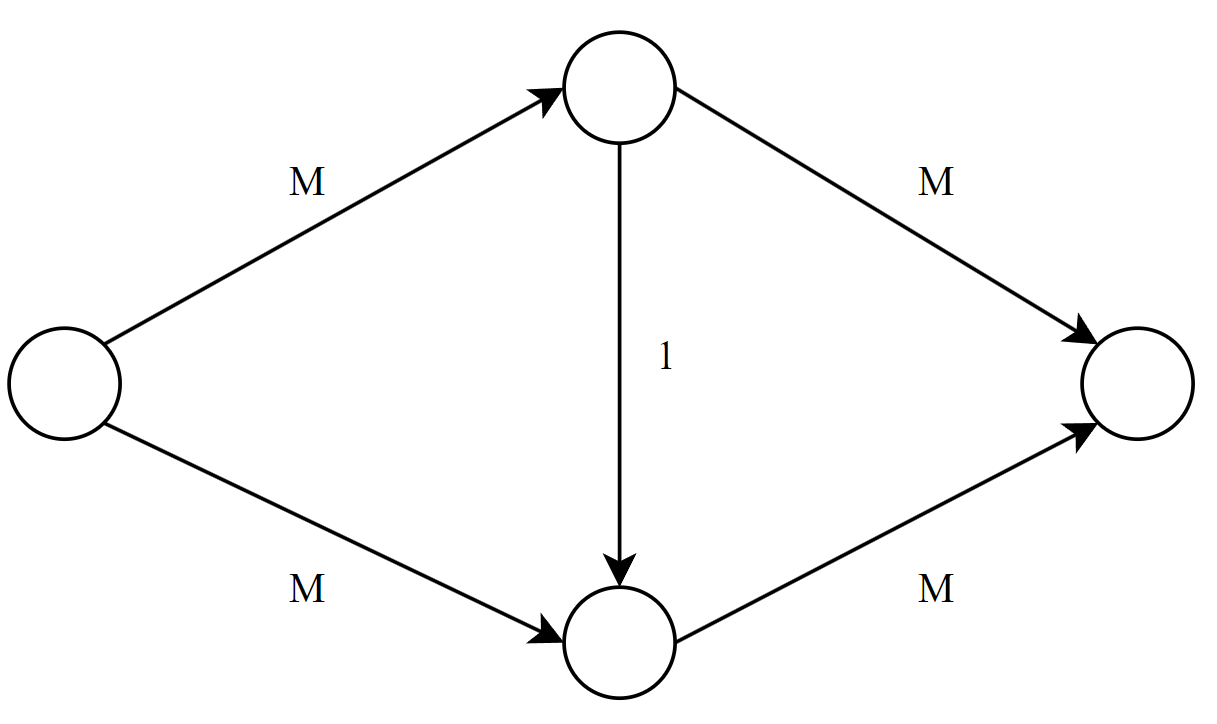
While the max flow is obviously $1$ in the graph above, our algorithm will keep on decreasing $M$ by $1$ in the residual graph until it’s gone, taking a total of $O(M)$ operations. Therefore the running time of this algorithm in the worst case is $O(nm*\max{c})$, where $n = |V|$ and $m = |E|$ (which I’ll use throughout this post). This is pseudo polynomial, which isn’t super great.

Later in 1972, the Edmond-Karp algorithm was created, which has a strongly polynomial time. The algorithm is similar to the algorithm, only we augment along the shortest path in $G(f)$. This small addition gives us the time complexity of $O(nm^2)$, independent of capacity. However, in 1971, a person called Dinic has already created a strongly polynomial time algorithm.

The Preflow - Push Algorithm

We now move on to a more efficient algorithm. This algorithm uses something called a preflow, so lets define that first.

Given a graph $G = (V,E)$ with directed edges, capacities $c : E \rightarrow \mathbb{R}_ {>0}$ and $s, t \in V$, $f : E \rightarrow \mathbb{R}_{>0}$ is called a preflow if it holds the following conditions:

$0 \leq f(e)\leq c(e) \quad ^\forall e \in E$
$e(v) = \sum_{e \in \delta^-(v)} f(e) - \sum_{e \in \delta^+(v)} f(e) \geq 0 \quad ^\forall v \in V/{s,t}$

Where $e(v)$ is called the excess of $v$. In addition, we define something called a label, along with a few additional terms:

$d : V \rightarrow \mathbb{Z}_0$ is called a label of a preflow $f$ if $^\forall e = (u,v) \in G(f)$, $d(u) \leq d(v)+1$
An edge $e = (u,v) \in G(f)$ is legitimate if $d(u) = d(v) + 1$
A node $v \in V/{s,t}$ is active if $e(v) > 0$

Now lets take a look at the algorithm.

Preflow - Push Algorithm

Initialization:
- $^\forall e = (s,u) \in E$, $f(e) = c(e)$
- $d(s) = n$, $d(t) = 0$, $^\forall v \in V/{s,t}$ $d(v) = 0$
while $^\exists$an active node $u$
- Push: $^\forall e = (u,v)$ legitimate in $G(f)$, push flow on $(u,v)$ with the amount $\min {u(e),e(u)}$
- Relabel: $d(u) = \min_{(u,v) \in G(f)} d(u) + 1$

Lets make two propositions from the algorithm above.

At all times the algorithm satisfies the condition of a preflow
When the algorithm stops, $f$ is a flow

The first proposition is easy to see. So is the second, as once the algorithm ends, there are no active nodes, meaning that all the excess values are $0$, and $f$ becomes a flow. Now lets show that this algorithm indeed finds the max flow in polynomial time.

Lemma: The shortest distance from $u$ to $v$ in $G(f)$ is lower-bounded by $d(u) - d(v)$

Proof: Let the path $P = i_0 - i_1 - \cdots - i_k$, where $u = i_0$ and $v = i_k$. Then because of the conditions of a label, we get the following inequalities.

\[\begin{align} d(i_0) - d&(i_1) \leq 1 \\ d(i_1) - d&(i_2) \leq 1 \\ &\vdots &\\ d(i_{k-1}) - d&(i_k) \leq 1 \end{align}\]

Adding all of these gives use the result $d(u) - d(v) = d(i_0) - d(i_k) \leq k$. $\blacksquare$

Lemma: If $u$ is active then $u$ has a directed directed path in $G(f)$ to $s$

Proof: Let $Y$ be the set of vertices not having a directed path to $s$. Suppose $u$ is active and $u \in Y$. Then, the following is true, since there all excess is greater or equal to zero, and there is at least one node who’s excess is greater than zero (i.e. active).

\[\sum_{v \in Y} \left( \sum_{e \in \delta^-(v)} f(e) - \sum_{e \in \delta^+(v)} f(e) \right) = \sum_{e \in \delta^-(Y)} f(e) - \sum_{e \in \delta^+(Y)} f(e) > 0\]

This means that there must be at least one edge in $\delta^-(Y)$ that has a positive amount of flow. Because an edge from $V/Y$ to $Y$ has positive flow, there exists an edge from $Y$ to $V/Y$ in $G(f)$, meaning there is a path from $Y$ to $V/Y$. However, since $Y$ is the set of all vertices that doesn’t have a path to $s$, any vertex in $V/Y$ has a path to $s$, leading to the fact that it is possible to reach $s$ from $Y$, which is a contradiction. $\blacksquare$

Corollary: A node $u \in V/{s,t}$ has $d(u) \leq 2n-1$

Proof: For $d(u)$ to increase $u$ has to be active, meaning there is a path to $s$. Since such path has a length of at most $n-1$, from the lemma above $d(u) - d(s) \leq n-1$, and because we initialized $d(s) = n$, we get the result $d(u) \leq 2n-1$. $\blacksquare$

Before we move on, lets define two types of pushes. A push is saturating if the amount is $u(e)$, and otherwise it is non-saturating.

With everything in place, we now show the running time of this algorithm.

Lemma: There can only be $O(n^2)$ relabeling operations

Proof: Trivial by the corollary. There are $n$ nodes, and $d(u)$ can increase up to $2n-1$, meaning there can only be up to $n(2n-1)$ relabeling operations. $\blacksquare$

Lemma: There are only $O(nm)$ saturating pushes

Proof: For a saturating push on $(u,v)$ to happen, $d(u) = d(v)+1$ must be true. To do another saturating push on this edge, the edge must be in the opposite direction, meaning $d(u) + 1 = d(v)$. In other words, between 2 consecutive saturating pushes from $u$ to $v$, $d(u)$ increases by at least $2$. Combining this with the corollary, we can perform a saturating push on a single edge $O(n)$ times for $O(m)$ edges, resulting in a total of $O(nm)$ saturating pushes. $\blacksquare$

Lemma: There are only $O(n^2m)$ non-saturating pushes

Proof: Lets define a potential $\Phi = \sum_{u \text{ is active}} d(u)$. We can make a few observations.

$\Phi$ goes up by $1$ due to relabeling
A saturating push can increase $\Phi$ when some node $v$ becomes active, which can happen at most $2n-1$ times.
$\Phi$ goes down by at least 1 when a non-saturating push is performed, since for an active vertex $u$, $e(u) > 0$ becomes $e(u) = 0$. Even if some new vertex $v$ becomes active, since $d(v)-d(u) = -1$, $\Phi$ always decreases.

Putting all of this together, $\Phi$ can increase at most $O(n^2)$ times from relabeling, and $cnm(2n-1)$ times by saturating pushes, where $c$ is some constant, resulting in a maximum of $O(n^2m)$ increases.

Since a non-saturating push always decreases $\Phi$, and $\Phi$ should result in $0$ at the end (and always positive), the number of non-saturating pushes will be at maximum the number of times $\Phi$ is increased. Therefore there can only be at most $O(n^2m)$ non-saturating pushes. $\blacksquare$

Putting together all of the lemmas, we conclude that there can be a total of $O(n^2)$ relabeling operations and a total of $O(n^2m)$ pushes, resulting in a total running time of $O(n^2m$).

Showing that the algorithm yields a max flow is simple after proving all the lemmas. If it weren’t the max flow, this would mean there is a path from $s$ to $t$ in $G(f)$. However the length of this path would be larger or equal to $d(s) - d(t) = n$, which is impossible.

In conclusion, the Preflow-Push algorithm finds the max flow in $O(n^2m)$ time.

Conclusion and Final Thoughts

This concludes the part about the max flow and min cut problem. The title says that, but most of this post talks about the preflow-push algorithm. Hopefully it doesn’t matter too much.

The algorithm explained in this post has a running time of $O(n^2m)$, but it can easily be modified to give a running time of $O(n^3)$. In fact, this is given in one of the problems. Other modifications can also give us a better time complexity. In addition, the current fastest algorithm for finding the max flow is $O(m^{1+o(1)})$.

I have known the existence of this algorithm for quite a while, but never put the time to actually learn it. Therefore I was glad to finally learn about it, Personally I found the proofs very interesting, and it was very satisfying to see all of them come together. This was all in the first day, and I thought it was a great start.

Now that’s done, here are the problems that were given, along with the rough solutions that I am aware of. There are a total six, but that’s only on the first day, and all other days there were 2~3 for each lecture.

Problems

Question 1: Consider the following variant of the min $s-t$ cut.

Given a graph $G = (V,E)$, terminals $s,t \in V$, and a capacity function on the edges $c : E \rightarrow \mathbb{R}_{>0}$. Find a cut $C \subset V$, so that $s \in C$, $t \notin C$, and we want to minimize

\[\sum_{e \in \delta^+(C)} c(e) - \sum_{e \in \delta^-(C)} c(e)\]

(Hint: this is an easier problem than the standard min $s-t$ cut).

Question 2: Given a flow $f$, let us define the width of the residual network $G(f)$ as

\[\max_{p \text{ is a } s-t \text{ path in } G(f)} \min_{e \in p} u(e)\]

where $u(e)$ is the capacity of edge $e$ in $G(f)$. Clearly the width is the maximum amount of flow we can augment “in one shot”, given $G(f)$. It is a very tempting idea to choose the path $G(f)$ that determines the width of $G(f)$, to do the augmentation.

True or False: if I augment $f$ along the path that determines the width of $G(f)$. In the next round, after this augmentation, is the width o the new residual network monotonically non-increasing?

Question 3: Suppose that in the town we have $r$ residents, $R_1, \cdots, R_r$; $c$ clubs $C_1 \cdots, C_c$, and $p$ political parties $P_1, \cdots, P_p$. A resident $R_i$ can belong to multiple clubs but only one particular party. We want to know : is it possible to let each club $C_j$ choose one of its members to represent it in the town council so that (1) no resident is a representative of two (or more) clubs, and (2) each party $P_k$ has at most $u_k$ representatives in that town council (remember that a chosen resident also belongs to a specific party).

Use the Max-flow network to answer the above question.

(In fact this is just the well-known Hall’s marriage theorem. Use Ford-Fulkerson max-flow-min-cut theorem to prove it).

Question 5: Consider the following variant of the preflow-push algorithm. In each iteration, we make a list of all active nodes. Then by non-increasing order of their distance labels, we examine them one by one. For the node in consideration, we keep pushing out its flow until it has no more excess or when we can relabel it. Once a relabeling operation happens, this iteration is over. In case that during an iteration, no node is ever re-labelled, we just stop the algorithm. Argue that this algorithm is correct and analyze the running time of this variant. (You can rule out the $O(n^2m)$ bound we have already discussed).

Question 6: Given a $s-t$ directed network $G = (V,E)$ with capacities $c : E \rightarrow \mathbb{R}_{>0}$.

Suppose that $X_1$ and $X_2$ are both min $s-t$ cuts (so $s \in X_1 \cap X_2$ and $t \notin X_1 \cup X_2$). Prove that $X_1 \cap X_2$, $X_1 \cup X_2$ are both min $s-t$ cuts as well.

Solutions

Some of these solutions could be incorrect.

1: We can know that the following is true by double-counting.

\[\sum_{e \in \delta^+(C)} c(e) - \sum_{e \in \delta^-(C)} c(e) = \sum_{v \in C} \left( \sum_{e \in \delta^+(v)} c(e) - \sum_{e \in \delta^-(v)} c(e) \right)\]

Therefore we just have to greedily select nodes where $\sum_{e \in \delta^+(v)} c(e) - \sum_{e \in \delta^-(v)} c(e)$ is negative.

2: False, the following image is a counterexample where the blue means the flow.

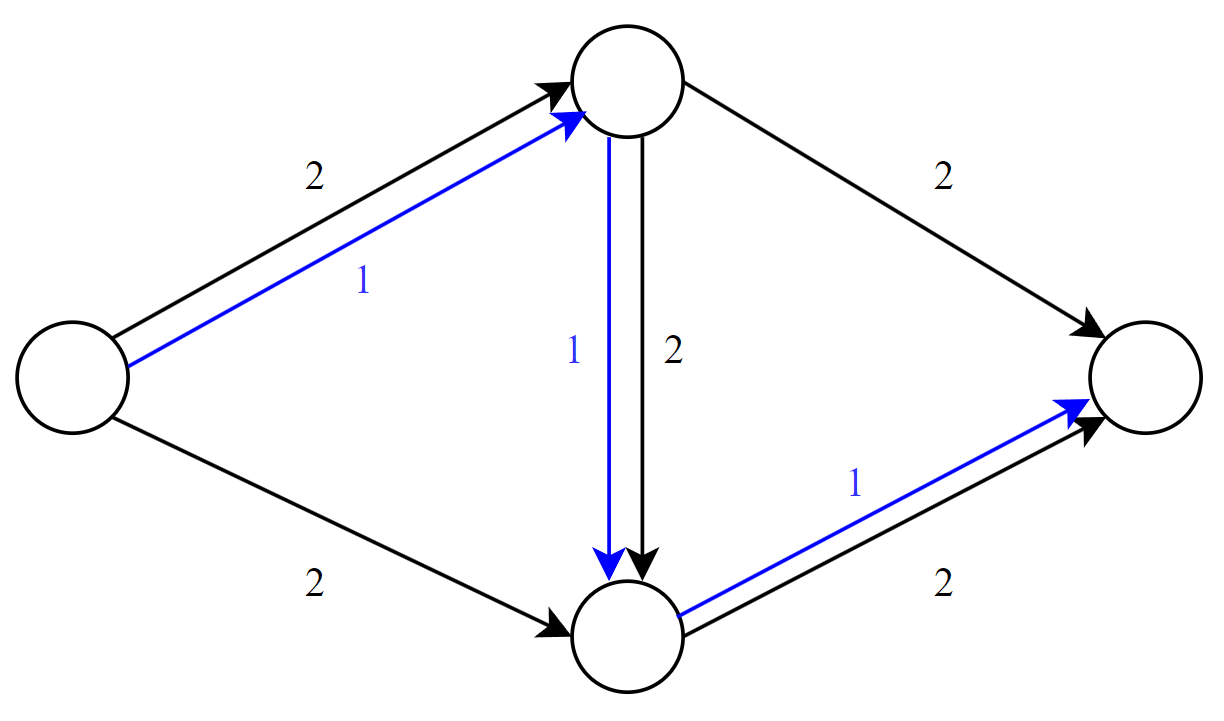
If we choose the blue path, which determines the width, and push an additional $1$, it is easy to see the width change to $2$, increasing the width.

3: Lets construct the following graph. All edges without specified capacities have a capacity of $1$.

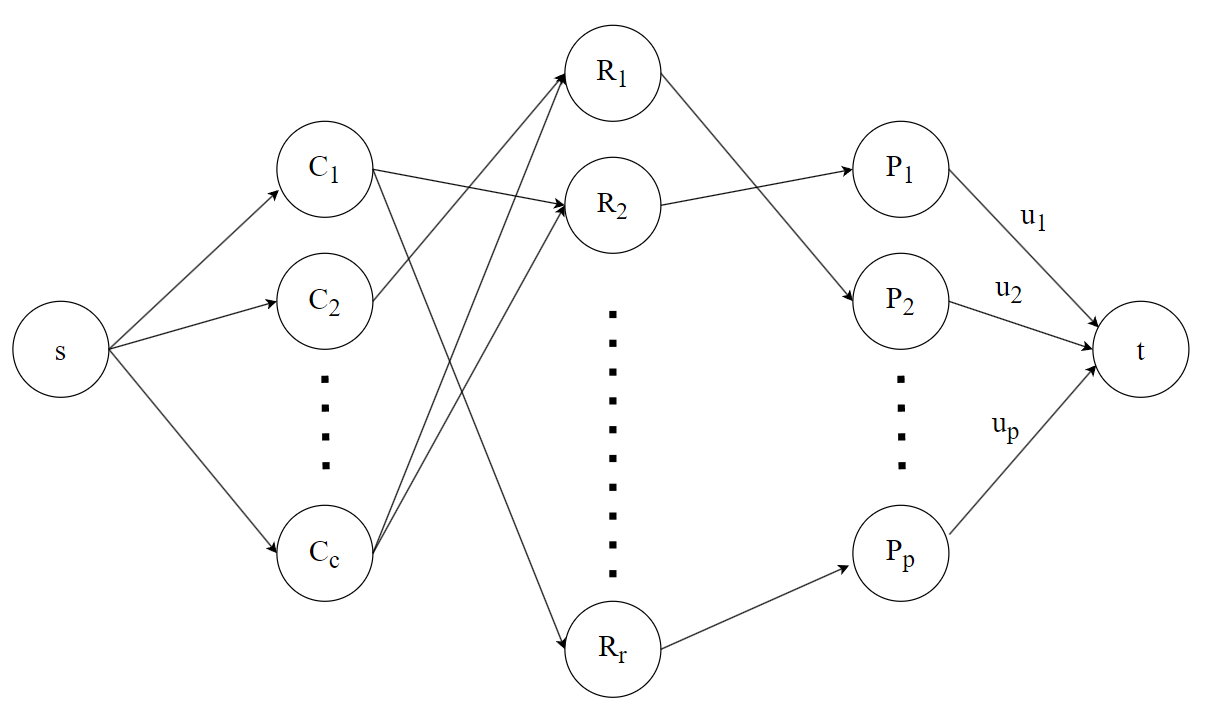
The edges between the second and third layer connect each resident with their clubs, and the edges between the third and fourth layer connect each resident with their political party. It is not hard to see that the condition in the problem can be satisfied when the max flow of the graph is $c$.

4: ($\rightarrow$) Since there exists a matching size of $|A|$, each vertex has at least $1$ distinct neighbor, meaning for any subset $A^\prime$ the number of neighbors is at least the size of $A^\prime$, which satisfies the condition.

5: I do not know the solution to this problem. However, I do know that the running time of the modified algorithm is $O(n^3)$. From what I have heard, this running time can be shown by showing that the total number of non-saturating pushes is reduced to $O(n)$ times per iteration, and that there are a total $O(n^2)$ iterations.

6: This can be solved easily by counting edges. We can divide the edges that contribute to the cut into the following categories based on the two vertices the edge connects.

$A$ and $B$
$A/B$ and $A \cap B$
$B/A$ and $A \cap B$
$A \cap B$ and $U/(A \cup B)$
$A/B$ and $U/(A \cup B)$
$B/A$ and $U/(A \cup B)$

It is easy to see that the edges of type 2 ~ 6 are contained on both $|X_1| + |X_2|$ and $|X_1 \cap X_2| + |X_1 \cup X_2|$. However, edges of type 1 are only contained in $|X_1| + |X_2|$. This leads to the inequality $|X_1| + |X_2| \geq |X_1 \cap X_2| + |X_1 \cup X_2|$. However, since $X_1$ and $X_2$ are both min-cuts, the value can’t be smaller, meaning they are equal. Therefore both $X_1 \cap X_2$ and $X_1 \cup X_2$ are also min-cuts.

Summer School Part 1 - Max Flow Min Cut Problem

Introduction

Problem Definition

The Residual Network

The Preflow - Push Algorithm

Conclusion and Final Thoughts

Problems

Solutions

See Also (WIP)

Further Reading

Persistent Segment Tree

Polygon Triangulation

Linear Programming and Duality