I have known about persistent segment trees for a while now. However I was only recently able to understand them well enough to use them. Here, I want to explain persistent segment trees in a way so that it is easy to know how they work, at least for me.
Introduction
A persistent data structure is a type of data structure that contains information for all past information, from the initial state, to all updates performed on them. In other words, a persistent segment tree is a segment tree that stores all the information for each update, like what value was added at what index and so on.
A naive approach would be to create a new segment tree for every update, but that would cost us $O(NlogN)$ space complexity per update, which is useless. Therefore, we have to think of a more efficient way.
The Structure
When we add a value in a segment tree, only $h = O(logN)$ nodes are updated. Therefore, instead of creating the whole tree from scratch, we can just add the $O(logN)$ vertices that have changed. Lets look at an example.
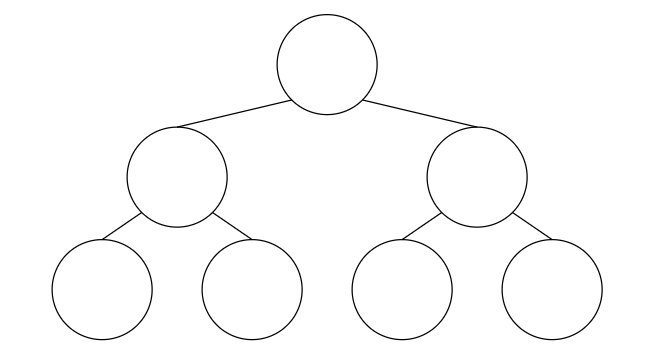
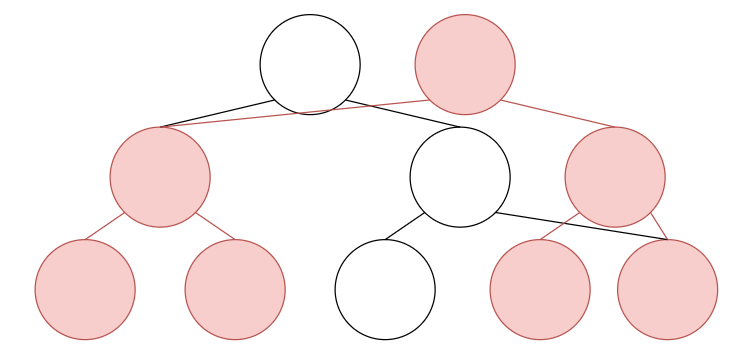
In the segment tree above, lets say we updated some nodes, colored in red
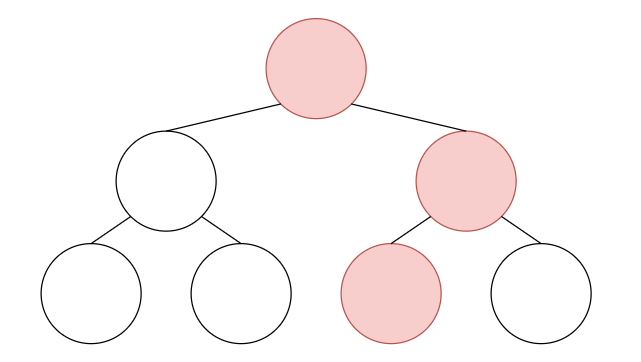
Since this data structure has to be persistent, instead of updating on the original segment tree, we have to add new nodes to preserve the previous state of the tree. Also, the new nodes should be connected in the same way they were in the original tree(the red edges).
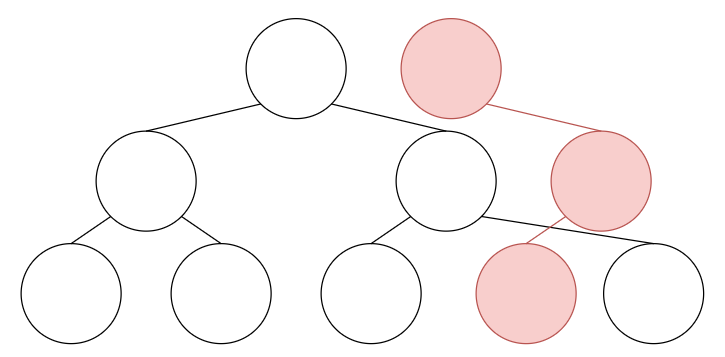
Finally, we should add some edges that connect the new nodes with the original tree. Basically we add an edge between a new node and the original tree where an update didn’t happen(the blue edges).
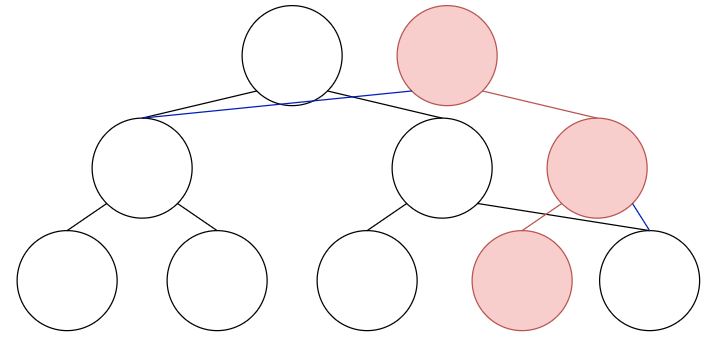
And we’re done! If start from the root of the new node and make our way down, we can see that we have successfully created a tree that has all the current updates, as well as the previous tree, only by adding $O(logN)$ (in this case 3) edges.
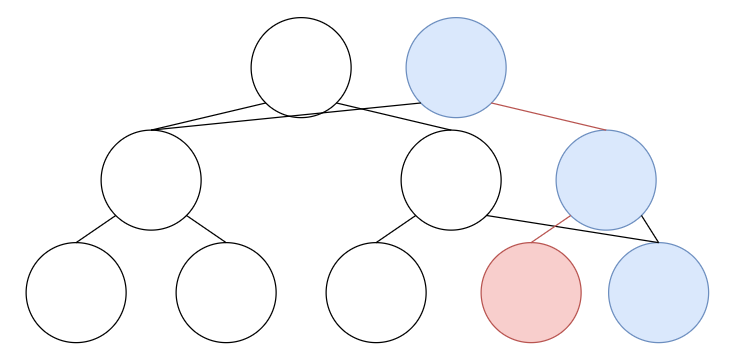
Using this process, we can repeatedly stack trees for every update that happens by only using $O(logN)$ memory. Just to make things clear, lets update the segment tree above one more time. This time we’re updating the blue nodes. Of course, we should modify the red part, as that was the latest update.
By adding the corresponding nodes, we get the following tree.
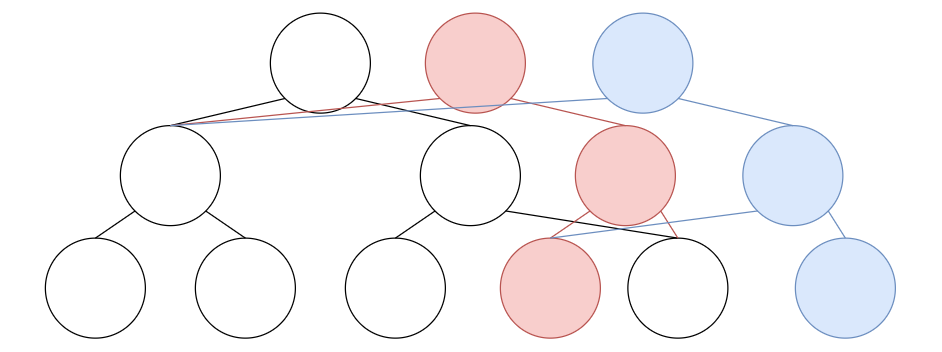
And in the same way with the red part, if go down starting from the blue root node, we get the tree corresponding to the third update.
Implementation
The implementation of a persistent segment tree with the update function can look something like this.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
const int N = 5e5+10LL;
struct PST{
#define lc t[cur].l
#define rc t[cur].r
struct node{
ll l = 0, r = 0, val = 0;
} t[20*N];
int T = 0;
int build(int s, int e){
int cur = ++T;
if(s==e) return cur;
ll m = (s+e)>>1;
lc = build(s,m);
rc = build(m+1,e);
t[cur].val = t[lc].val+t[rc].val;
return cur;
}
int upd(int pre, int s, int e, int i, ll v){
int cur = ++T;
t[cur] = t[pre];
if(s==e){
t[cur].val += v;
return cur;
}
ll m = (s+e)>>1;
if(i<=m){
rc = t[pre].r;
lc = upd(t[pre].l,s,m,i,v);
}
else{
lc = t[pre].l;
rc = upd(t[pre].r,m+1,e,i,v);
}
t[cur].val = t[lc].val+t[rc].val;
return cur;
}
};
Unlike a regular segment tree, each node in a persistent segment tree is defined as a struct that stores the node number of the left and right child of the node, as well as the value stored in that node.
The build function is a function that builds the very first tree. When the build function is called, it creates a new node, giving it a new index which can be found with $T$. At the end of the function, it returns the index of the newly made node, which is used as the index of the left and right child in another iteration. Note that the index of the root node of the first tree($root[0]$) is equal to $build(1,N)$.
In the update function, we pass in the index of the root node of the tree we want to update on. Then we proceed by creating a new node, then set the new node equal to corresponding node of the previous tree. After that, based on the index we want to update, we recursively create the right child and left child. Also, like the build function, we return the index of the current node. The update process can look something like the image below.

Now that the implementation is done, lets see where this thing is actually used.
Queries
Range Sum
PST’s can be used to perform 2 dimensional queries in a rectangular area. Consider the problem where we are given some number of points and must count the number of points contained in a rectangular area. For simplicity we are going to assume no two points have the same $x$-coordinate.
We’re going to solve this problem using PST(obviously). We are going to update the PST by adding the points in order of increasing $x$-coordinate. Also, the index we are updating will be the $y$-coordinate of the point. Then the $i^{th}$ segment tree contains information up to the $i^{th}$ point.
When we’re given a rectangular range, we can find the range of points that fall into the $x$-coordinate of the rectangle. Lets say the $l$~$r^{th}$ points have the correct $x$-coordinates. To find the points with the correct $y$-coordinate range(lets say $y_1$~$y_2$) we can simply perform a range sum query on a segment tree.
Performing a range sum($y_1$~$y_2$) on the $i^{th}$ segment tree gives us the number of points with a $y$-coordinate in the range of $y_1$~$y_2$ up to the $i^{th}$ point. Lets call this function $sum(i,y_1,y_2)$. Then to find the wanted points in the range $l$~$r$, all we have to do is find $sum(l,y_1,y_2)-sum(r-1,y_1,y_2)$.
The implementation can look something like this.
1
2
3
4
5
6
7
8
9
10
ll psum(int cur, int s, int e, int l, int r){
if(r<s||l>e) return 0;
if(l<=s&&e<=r) return t[cur].val;
ll m = (s+e)>>1;
return psum(lc,s,m,l,r)+psum(rc,m+1,e,l,r);
}
ll sum(int pre, int cur, int s, int e, int l, int r){
return psum(cur,s,e,l,r)-psum(pre,s,e,l,r);
}
$k^{th}$ Number
Another query we can solve, using the range sum query explained above, is to find the $k^{th}$ smallest number in a certain range in an array. For each element in the array, we can correspond them to a point whose $x$-coordinate is the index, and the $y$-coordinate is the value.
Like we have discussed before, we can find the number of points in a certain range. What we can do is start from the root node, which has the number of points in the full $y$-coordinate range, then binary search our way to find the $k^{th}$ smallest number.
The implementation can look something like this.
1
2
3
4
5
6
7
int kth(int pre, int cur, int s, int e, int k){
if(s==e) return s;
int cnt = t[lc].val-t[t[pre].l].val;
ll m = (s+e)>>1;
if(cnt>=k) return kth(t[pre].l,lc,s,m,k);
else return kth(t[pre].r,rc,m+1,e,k-cnt);
}
Conclusion
So this is a brief introduction on persistent segment trees. Once understood, they are pretty straightforward to use. I’ll end this post with some practice problems. Some of them are in Korean.
- Egg: Problem Link
- A problem to count the number of points in a certain range
- K-th Number: Problem Link
- Self explanatory, find the k-th smallest number in a certain range
- XOR 쿼리: Problem Link
- Perform various queries using PST
